Radix Sort

Last translate with upstream: 08eb0c5

This article will briefly introduce radix sort.

Introduction

Radix sort is a non-comparative sorting algorithm. It came into common use as a way to sort punched cards in early times.

The working principles is that the algorithm splits the elements to be sorted into k keywords (when comparing two elements, first compare the first keyword, if they are the same, then compare the second keyword...), and then stably sort the k th keywords, the k-1 -th keywords, and then sort the k-2 -th keywords... Finally, sort the first keywords stably, and the stable sorting of the entire sequence is completed.

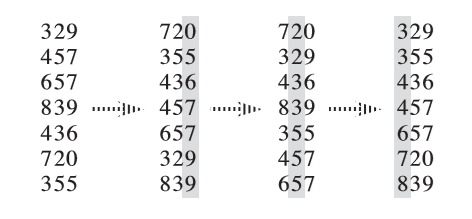
An illustrated process of radix sort

Radix sort needs to use a stable algorithm in order to sort inner keywords.

Generally, radix sorting is faster than sorting comparison-based algorithm (e.g. quicksort). However, because of the need of extra memory, when the memory space is low, in-place algorithm (e.g. quicksort) may be a better choice.1

For the correctness of radix sort, you can refer to the solution of Introduction to Algorithm exercise 8.3-3.

Properties

Stability

Radix sort is a stable sorting algorithm.

Time Complexity

In general, if the range of each keyword is not large, you can use counting sort as the inner sorting. The time complexity is O(nk+\sum\limits_{i= 1}^k w_i) , where w_i is the range of the i th keyword. If the key value range is large, you can directly use the comparison-based sorting algorithm with the time complexity of O(nk\log n) without using radix sort.

Space Complexity

The space complexity of radix sort is O(k+n)

Code Implementations

Pseudocode

\begin{array}{ll} 1 & \textbf{Input. } \text{An array } A \text{ consisting of }n\text{ elements, where each element has }k\text{ keys.}\\ 2 & \textbf{Output. } \text{Array }A\text{ will be sorted in nondecreasing order stably.} \\ 3 & \textbf{Method. } \\ 4 & \textbf{for }i\gets k\textbf{ down to }1\\ 5 & \qquad\text{sort }A\text{ into nondecreasing order by the }i\text{-th key stably} \end{array}

C++ code:

const int N = 100010;
const int W = 100010;
const int K = 100;

int n, w[K], k, cnt[W];

struct Element {
  int key[K];
  bool operator<(const Element& y) const {
    // how two elements are compared
    for (int i = 1; i <= k; ++i) {
      if (key[i] == y.key[i]) continue;
      return key[i] < y.key[i];
    }
    return false;
  }
} a[N], b[N];

void counting_sort(int p) {
  memset(cnt, 0, sizeof(cnt));
  for (int i = 1; i <= n; ++i) ++cnt[a[i].key[p]];
  for (int i = 1; i <= w[p]; ++i) cnt[i] += cnt[i - 1];
  // To ensure the stability of sorting algorithm, the looping of $i$ here 
  // should begin from $n$ to $1$.
  // I.e., if the keyword of two elements is the same, the element came before
  // the other originally should still come before the other after sorting.
  for (int i = 1; i <= n; ++i) b[cnt[a[i].key[p]]--] = a[i];
  memcpy(a, b, sizeof(a));
}

void radix_sort() {
  for (int i = k; i >= 1; --i) {
    // Sort keywords by using counting sort.
    counting_sort(i);
  }
}

References and Footnotes

  1. Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein.Introduction to Algorithms(3rd ed.). MIT Press and McGraw-Hill, 2009. ISBN 978-0-262-03384-8. "8.3 Radix sort", pp. 199. ↩

buildLast update and/or translate time of this article，Check the history
editFound smelly bugs? Translation outdated? Wanna contribute with us? Edit this Page on Github
peopleContributor of this article OI-wiki
translateTranslator of this article Visit the original article!
copyrightThe article is available under CC BY-SA 4.0 & SATA ; additional terms may apply.

Comments