Stern-Brocot Tree & Farey Sequence

Stern-Brocot tree¶

The Stern-Brocot tree is an elegant data structure for maintaining positive fractions. It was discovered independently by Moritz Stern in 1858 and Achille Brocot in 1861.

Overview¶

The Stern-Borcot tree starts with two simple fractions:

This may make you feel a little confused. But we will not discuss its preciseness here. You can just treat it as .

Every time we insert a fraction between two adjacent fractions , which means one iteration is completed and the next sequence is obtained. So it will look like this.

Since we call this data structure Stern-Brocot tree, it must look like a tree, right? Look at this figure:

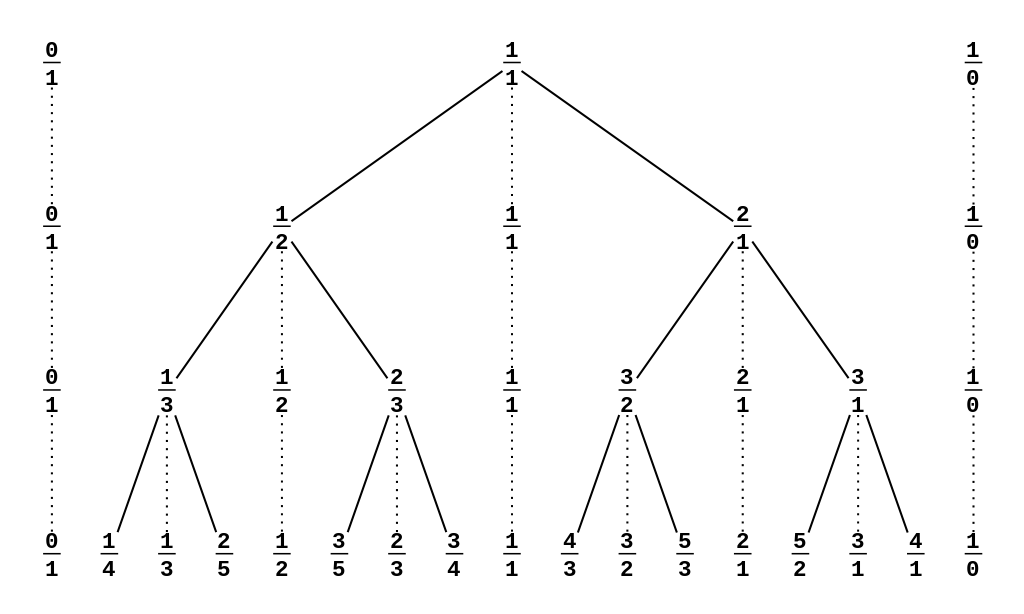
You can think of the sequence at the level as an in-order traversal of the Stern-Brocot tree with a depth of .

Property¶

Next, let's discuss the property of the Stern-Brocot tree.

Monotonicity¶

In the sequence of each layer, the true fraction is monotonically increasing.

Brief proof: only need to prove in the case of

That's it. This is very easy, we can just do algebraic transformation directly

The same is true on the other side.

Irreducibility¶

The fractions in the sequence (except for ) are the irreducible fraction.

Brief proof: To prove the irreducibility, we first prove that for two consecutive fractions in the sequence :

Obviously, we only need to prove that under the condition of .

The latter part is the same. we can prove using the extended Euclidean theorem. If the above equation has a solution, obviously . Then the proof is finished.

With the above proof, we can prove .

With these two properties, you can treat it as a balanced tree. So we can construct and query the same way we do to the balanced trees.

Implementation¶

Construct:

void build(int a = 0, int b = 1, int c = 1, int d = 0, int level = 1) {
  int x = a + c, y = b + d;
  // ... output the current fraction x/y
  // at the current level in the tree
  build(a, b, x, y, level + 1);
  build(x, y, c, d, level + 1);
}

Query:

string find(int x, int y, int a = 0, int b = 1, int c = 1, int d = 0) {
  int m = a + c, n = b + d;
  if (x == m && y == n) return "";
  if (x * n < y * m)
    return 'L' + find(x, y, a, b, m, n);
  else
    return 'R' + find(x, y, m, n, c, d);
}

Farey sequence¶

Stern-Brocot tree and Farey sequence have very similar characteristics. The -th Farey sequence is denoted as , which means that all the simplest true fractions whose denominator is less than or equal to are arranged in order of value.

Obviously, the above algorithm for constructing Stern-Brocot tree is also suitable for constructing the Farey sequence. Because the numbers in the Stern-Brocot tree are the irreducible fraction, a slight modification of the boundary conditions (denominator) can form the code for constructing the Farey sequence. You can think the Farey sequence as a subsequence of the sequence obtained after the -th iteration of Stern-Brocot.

The Farey sequence also satisfies the irreducibility and monotonicity, and satisfies a property similar to the Stern-Brocot tree: for the three consecutive numbers in the sequence, there is . This can be easily proved, so we won't repeat it here.

From the definition of Farey sequence, we can get the length of . The formula of is:

This page is mainly translated from the blog post Дерево Штерна-Броко. Ряд Фарея and its English version The Stern-Brocot Tree and Farey Sequences. The license for the Russian version is Public Domain + Leave a Link; the license for the English version is CC-BY-SA 4.0.

Last update and/or translate time of this article，Check the history
Found smelly bugs? Translation outdated? Wanna contribute with us? Edit this Page on Github
Contributor of this article OI-wiki
Translator of this article Visit the original article!
The article is available under CC BY-SA 4.0 & SATA ; additional terms may apply.

Stern-Brocot Tree & Farey Sequence