DP on DAG
DAG 即 有向无环图,一些实际问题中的二元关系都可使用 DAG 来建模。
例子¶
以这道题为例子,来分析一下 DAG 建模的过程。
例题 UVa 437 巴比伦塔 The Tower of Babylon
有
建立 DAG¶
由于每个砖块的底面长宽分别严格小于它下方砖块的底面长宽,因此不难将这样一种关系作为建图的依据,而本题也就转化为最长路问题。
也就是说如果砖块
本题的另一个问题在于每个砖块的高有三种选法,怎样建图更合适呢?
不妨将每个砖块拆解为三种堆叠方式,即将一个砖块分解为三个砖块,每一个拆解得到的砖块都选取不同的高。
初始的起点是大地,大地的底面是无穷大的,则大地可达任意砖块,当然我们写程序时不必特意写上无穷大。
假设有两个砖块,三条边分别为 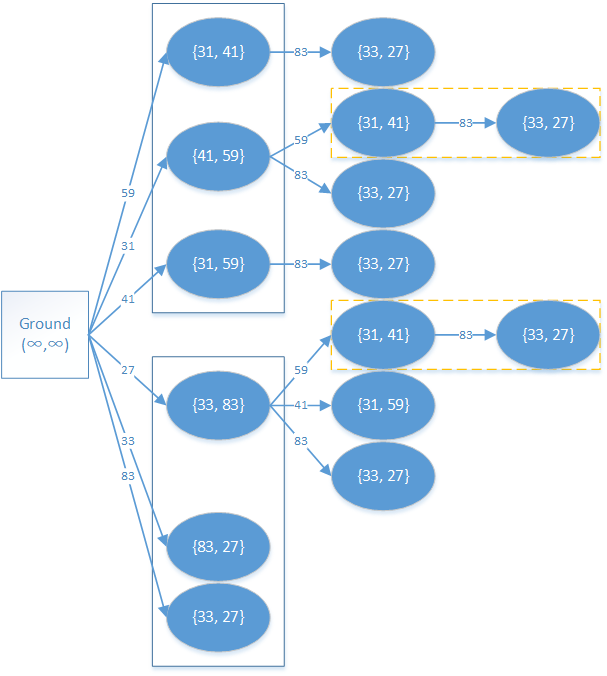
图中蓝实框所表示的是一个砖块拆解得到的一组砖块,之所以用
图中黄虚框表示的是重复计算部分,为下文做铺垫。
转移¶
题目要求的是塔的最大高度,已经转化为最长路问题,其起点上文已指出是大地,那么终点呢?
显然终点已经自然确定,那就是某砖块上不能再搭别的砖块的时候。
之前在图上标记的黄虚框表明有重复计算,下面我们开始考虑转移方程。
显然,砖块一旦选取了高,那么这块砖块上最大能放的高度是确定的。
某个砖块
其中
在实际编写时,将所有
在试图计算前,如果发现已经计算过,直接返回保存的值;否则就按步计算,并保存。
最终答案是所有
题解¶
#include <cstring>
#include <iostream>
#define MAXN (30 + 5)
#define MAXV (500 + 5)
#define MAX(a, b) (((a) > (b)) ? (a) : (b))
int d[MAXN][3];
int x[MAXN], y[MAXN], z[MAXN];
int babylon_sub(int c, int rot, int n) {
if (d[c][rot] != -1) {
return d[c][rot];
}
d[c][rot] = 0;
int base1, base2;
if (rot == 0) {
base1 = x[c];
base2 = y[c];
}
if (rot == 1) {
base1 = y[c];
base2 = z[c];
}
if (rot == 2) {
base1 = x[c];
base2 = z[c];
}
for (int i = 0; i < n; i++) {
if ((x[i] < base1 && y[i] < base2) || (y[i] < base1 && x[i] < base2))
d[c][rot] = MAX(d[c][rot], babylon_sub(i, 0, n) + z[i]);
if ((y[i] < base1 && z[i] < base2) || (z[i] < base1 && y[i] < base2))
d[c][rot] = MAX(d[c][rot], babylon_sub(i, 1, n) + x[i]);
if ((x[i] < base1 && z[i] < base2) || (z[i] < base1 && x[i] < base2))
d[c][rot] = MAX(d[c][rot], babylon_sub(i, 2, n) + y[i]);
}
return d[c][rot];
}
int babylon(int n) {
for (int i = 0; i < n; i++) {
d[i][0] = -1;
d[i][1] = -1;
d[i][2] = -1;
}
int r = 0;
for (int i = 0; i < n; i++) {
r = MAX(r, babylon_sub(i, 0, n) + z[i]);
r = MAX(r, babylon_sub(i, 1, n) + x[i]);
r = MAX(r, babylon_sub(i, 2, n) + y[i]);
}
return r;
}
int main() {
int t = 0;
while (true) {
int n;
std::cin >> n;
if (n == 0) break;
t++;
for (int i = 0; i < n; i++) {
std::cin >> x[i] >> y[i] >> z[i];
}
std::cout << "Case " << t << ":"
<< " maximum height = " << babylon(n);
std::cout << std::endl;
}
return 0;
}buildLast update and/or translate time of this article,Check the history
editFound smelly bugs? Translation outdated? Wanna contribute with us? Edit this Page on Github
peopleContributor of this article OI-wiki
translateTranslator of this article Visit the original article!
copyrightThe article is available under CC BY-SA 4.0 & SATA ; additional terms may apply.