Sparse Table

简介

ST 表是用于解决 可重复贡献问题 的数据结构。

什么是可重复贡献问题？

可重复贡献问题 是指对于运算 \operatorname{opt} ，满足 x\operatorname{opt} x=x ，则对应的区间询问就是一个可重复贡献问题。例如，最大值有 \max(x,x)=x ，gcd 有 \operatorname{gcd}(x,x)=x ，所以 RMQ 和区间 GCD 就是一个可重复贡献问题。像区间和就不具有这个性质，如果求区间和的时候采用的预处理区间重叠了，则会导致重叠部分被计算两次，这是我们所不愿意看到的。另外， \operatorname{opt} 还必须满足结合律才能使用 ST 表求解。

什么是RMQ？

RMQ 是英文 Range Maximum/Minimum Query 的缩写，表示区间最大（最小）值。解决 RMQ 问题有很多种方法，可以参考 RMQ 专题。

引入

ST 表模板题

题目大意：给定 n 个数，有 m 个询问，对于每个询问，你需要回答区间 [l,r] 中的最大值。

考虑暴力做法。每次都对区间 [l,r] 扫描一遍，求出最大值。

显然，这个算法会超时。

ST 表

ST 表基于 倍增 思想，可以做到 \Theta(n\log n) 预处理， \Theta(1) 回答每个询问。但是不支持修改操作。

基于倍增思想，我们考虑如何求出区间最大值。可以发现，如果按照一般的倍增流程，每次跳 2^i 步的话，询问时的复杂度仍旧是 \Theta(\log n) ，并没有比线段树更优，反而预处理一步还比线段树慢。

我们发现 \max(x,x)=x ，也就是说，区间最大值是一个具有“可重复贡献”性质的问题。即使用来求解的预处理区间有重叠部分，只要这些区间的并是所求的区间，最终计算出的答案就是正确的。

如果手动模拟一下，可以发现我们能使用至多两个预处理过的区间来覆盖询问区间，也就是说询问时的时间复杂度可以被降至 \Theta(1) ，在处理有大量询问的题目时十分有效。

具体实现如下：

令 f(i,j) 表示区间 [i,i+2^j-1] 的最大值。

显然 f(i,0)=a_i 。

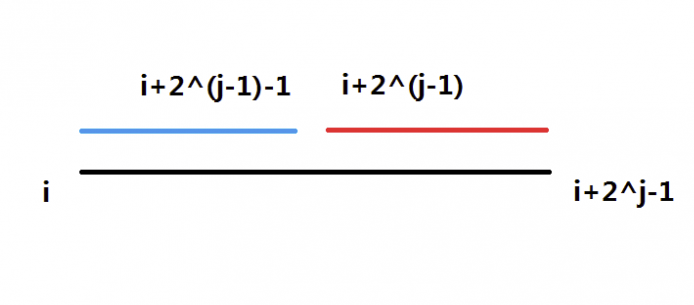
根据定义式，第二维就相当于倍增的时候“跳了 2^j-1 步”，依据倍增的思路，写出状态转移方程： f(i,j)=\max(f(i,j-1),f(i+2^{j-1},j-1)) 。

以上就是预处理部分。而对于查询，可以简单实现如下：

对于每个询问 [l,r] ，我们把它分成两部分： f[l,l+2^s-1] 与 f[r-2^s+1,r] 。

其中 s=\left\lfloor\log_2(r-l+1)\right\rfloor 。

根据上面对于“可重复贡献问题”的论证，由于最大值是“可重复贡献问题”，重叠并不会对区间最大值产生影响。又因为这两个区间完全覆盖了 [l,r] ，可以保证答案的正确性。

模板代码

ST 表模板题

#include <bits/stdc++.h>
using namespace std;
const int logn = 21;
const int maxn = 2000001;
int f[maxn][logn + 1], Logn[maxn + 1];
inline int read() {
  char c = getchar();
  int x = 0, f = 1;
  while (c < '0' || c > '9') {
    if (c == '-') f = -1;
    c = getchar();
  }
  while (c >= '0' && c <= '9') {
    x = x * 10 + c - '0';
    c = getchar();
  }
  return x * f;
}
void pre() {
  Logn[1] = 0;
  Logn[2] = 1;
  for (int i = 3; i < maxn; i++) {
    Logn[i] = Logn[i / 2] + 1;
  }
}
int main() {
  int n = read(), m = read();
  for (int i = 1; i <= n; i++) f[i][0] = read();
  pre();
  for (int j = 1; j <= logn; j++)
    for (int i = 1; i + (1 << j) - 1 <= n; i++)
      f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
  for (int i = 1; i <= m; i++) {
    int x = read(), y = read();
    int s = Logn[y - x + 1];
    printf("%d\n", max(f[x][s], f[y - (1 << s) + 1][s]));
  }
  return 0;
}

注意点

  1. 输入输出数据一般很多，建议开启输入输出优化。

  2. 每次用 std::log 重新计算 log 函数值并不值得，建议进行如下的预处理：

\left\{\begin{aligned} Logn[1] &=0, \\ Logn\left[i\right] &=Logn[\frac{i}{2}] + 1. \end{aligned}\right.

ST 表维护其他信息

除 RMQ 以外，还有其它的“可重复贡献问题”。例如“区间按位和”、“区间按位或”、“区间 GCD”，ST 表都能高效地解决。

需要注意的是，对于“区间 GCD”，ST 表的查询复杂度并没有比线段树更优（令值域为 w ，ST 表的查询复杂度为 \Theta(\log w) ，而线段树为 \Theta(\log n+\log w) ，且值域一般是大于 n 的），但是 ST 表的预处理复杂度也没有比线段树更劣，而编程复杂度方面 ST 表比线段树简单很多。

如果分析一下，“可重复贡献问题”一般都带有某种类似 RMQ 的成分。例如“区间按位与”就是每一位取最小值，而“区间 GCD”则是每一个质因数的指数取最小值。

总结

ST 表能较好的维护“可重复贡献”的区间信息（同时也应满足结合律），时间复杂度较低，代码量相对其他算法很小。但是，ST 表能维护的信息非常有限，不能较好地扩展，并且不支持修改操作。

练习

RMQ 模板题

「SCOI2007」降雨量

[USACO07JAN]平衡的阵容 Balanced Lineup

附录：ST 表求区间 GCD 的时间复杂度分析

在算法运行的时候，可能要经过 \Theta(\log n) 次迭代。每一次迭代都可能会使用 GCD 函数进行递归，令值域为 w ，GCD 函数的时间复杂度最高是 \Omega(\log w) 的，所以总时间复杂度看似有 O(n\log n\log w) 。

但是，在 GCD 的过程中，每一次递归（除最后一次递归之外）都会使数列中的某个数至少减半，而数列中的数最多减半的次数为 \log_2 (w^n)=\Theta(n\log w) ，所以，GCD 的递归部分最多只会运行 O(n\log w) 次。再加上循环部分（以及最后一层递归）的 \Theta(n\log n) ，最终时间复杂度则是 O(n(\log w+\log x)) ，由于可以构造数据使得时间复杂度为 \Omega(n(\log w+\log x)) ，所以最终的时间复杂度即为 \Theta(n(\log w+\log x)) 。

而查询部分的时间复杂度很好分析，考虑最劣情况，即每次询问都询问最劣的一对数，时间复杂度为 \Theta(\log w) 。因此，ST 表维护“区间 GCD”的时间复杂度为预处理 \Theta(n(\log n+\log w)) ，单次查询 \Theta(\log w) 。

线段树的相应操作是预处理 \Theta(n\log x) ，查询 \Theta(n(\log n+\log x)) 。

这并不是一个严谨的数学论证，更为严谨的附在下方：

更严谨的证明

理解本段，可能需要具备 时间复杂度 的关于“势能分析法”的知识。

先分析预处理部分的时间复杂度：

设“待考虑数列”为在预处理 ST 表的时候当前层循环的数列。例如，第零层的数列就是原数列，第一层的数列就是第零层的数列经过一次迭代之后的数列，即 st[1..n][1]，我们将其记为 A 。

而势能函数就定义为“待考虑数列”中所有数的累乘的以二为底的对数。即： \Phi(A)=\log_2\left(\prod\limits_{i=1}^n A_i\right) 。

在一次迭代中，所花费的时间相当于迭代循环所花费的时间与 GCD 所花费的时间之和。其中，GCD 花费的时间有长有短。最短可能只有两次甚至一次递归，而最长可能有 O(\log w) 次递归。但是，GCD 过程中，除最开头一层与最末一层以外，每次递归都会使“待考虑数列”中的某个结果至少减半。即， \Phi(A) 会减少至少 1 ，该层递归所用的时间可以被势能函数均摊。

同时，我们可以看到， \Phi(A) 的初值最大为 \log_2 (w^n)=\Theta(n\log w) ，而 \Phi(A) 不增。所以，ST 表预处理部分的时间复杂度为 O(n(\log w+\log n)) 。

buildLast update and/or translate time of this article，Check the history
editFound smelly bugs? Translation outdated? Wanna contribute with us? Edit this Page on Github
peopleContributor of this article OI-wiki
translateTranslator of this article Visit the original article!
copyrightThe article is available under CC BY-SA 4.0 & SATA ; additional terms may apply.

Comments